How many pattern block rhombuses would create 4 hexagons sets the stage for a fascinating exploration into the world of geometry and pattern blocks. This investigation delves into the relationship between rhombuses and hexagons, revealing how these shapes can be combined to create larger, more complex structures. By understanding the fundamental principles of shape and pattern, we can unlock a world of possibilities in design and problem-solving.
Pattern blocks are a versatile tool for learning about geometric shapes and their properties. Each block represents a different shape, such as a square, triangle, rhombus, or hexagon. By manipulating these blocks, we can explore concepts like symmetry, area, and perimeter in a hands-on and engaging way. This exploration will focus on the relationship between rhombuses and hexagons, specifically investigating how many rhombuses are needed to construct a hexagon.
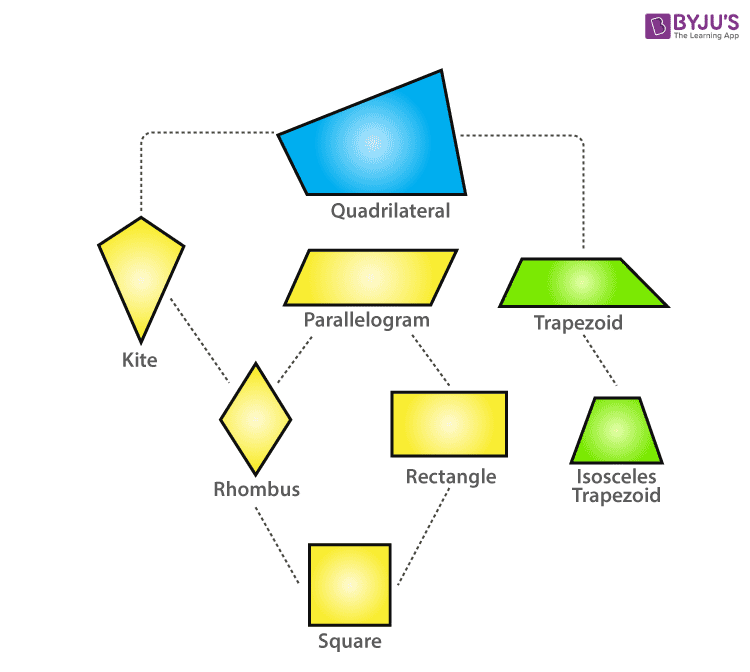
Understanding Shapes
Let’s dive into the fascinating world of shapes and explore the relationship between rhombuses and hexagons. These two geometric figures might seem different at first glance, but there’s a hidden connection that makes them perfect partners in the world of pattern blocks.
Rhombus and Hexagon: A Tale of Sides and Angles, How many pattern block rhombuses would create 4 hexagons
The rhombus and hexagon are both polygons, meaning they are closed figures formed by straight line segments. A rhombus is a four-sided shape with all sides equal in length. A hexagon is a six-sided shape with all sides equal in length. A rhombus has four angles, and a hexagon has six angles. A rhombus has two acute angles and two obtuse angles, while a hexagon has six equal angles.
The difference between the two lies in the number of sides and angles, which leads to a unique relationship between them.
Visual Representation: A Side-by-Side Comparison
Imagine a rhombus and a hexagon standing side by side. The rhombus, with its four equal sides and four angles, looks like a tilted square. The hexagon, on the other hand, is a six-sided figure with six equal angles. Although they differ in the number of sides and angles, they share a common characteristic: all their sides are equal in length.
Fitting Rhombuses Within a Hexagon
The number of rhombuses that can fit within a hexagon is a bit of a puzzle. Think of the hexagon as a beehive, and each rhombus as a honeycomb cell. You can fit six rhombuses within a hexagon, creating a beautiful and symmetrical pattern. Each rhombus perfectly fills a section of the hexagon, forming a complete and harmonious design.
This arrangement highlights the harmonious relationship between these two shapes.
Pattern Block Exploration
Get ready to dive into the wonderful world of pattern blocks! These colorful shapes are more than just toys; they’re a gateway to understanding geometric concepts and exploring creativity.
Pattern Block Shapes and Colors
Pattern blocks come in a variety of shapes and colors, each with its unique properties. These shapes are essential for building different geometric figures, including hexagons.
- Green Triangle: This equilateral triangle has three equal sides and three equal angles, each measuring 60 degrees. It’s a fundamental building block for many shapes.
- Orange Square: This square has four equal sides and four right angles (90 degrees). It’s a familiar shape that forms the basis of many designs.
- Blue Rhombus: This rhombus has four equal sides but two different angles. It’s a versatile shape that can be used to create a variety of patterns.
- Red Trapezoid: This trapezoid has two parallel sides of different lengths. It’s a unique shape that adds variety to your creations.
- Yellow Hexagon: This hexagon has six equal sides and six equal angles. It’s a key shape for exploring symmetry and tessellations.
Building a Hexagon with Pattern Blocks
Constructing a hexagon with pattern blocks is a fun and engaging activity. You can create a hexagon using various combinations of pattern blocks, but the most common method involves using rhombuses.
To build a hexagon, you need six rhombuses.
Place the rhombuses side by side, ensuring that the longer sides of each rhombus touch. The resulting shape will be a hexagon.
Pattern Block Hexagon Table
Let’s take a closer look at the rhombuses used to build a hexagon and organize the information in a table.
| Rhombus Color | Rhombus Shape | Number of Rhombuses | Hexagon Shape |
|---|---|---|---|
| Blue | Rhombus | 6 | Regular Hexagon |
Building a Hexagon
We’re ready to dive into the fascinating world of hexagons using our trusty pattern block rhombuses! Let’s learn how to construct a hexagon using these colorful shapes.
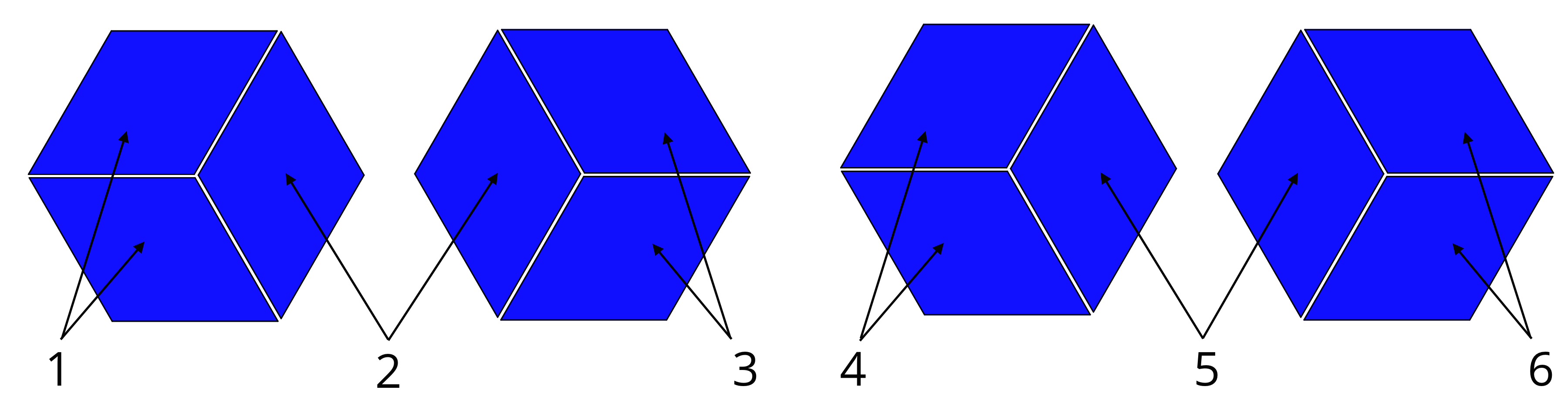
The pattern block rhombus is a versatile shape that can be used to build many different geometric figures. It’s like a building block for shapes! One of the cool things about rhombuses is that they can be arranged to form a hexagon, which is a six-sided shape with equal sides and angles. Let’s see how it’s done.
Arrangement of Rhombuses in a Hexagon
A hexagon can be built using six rhombuses. To create a hexagon, arrange the rhombuses in a circular pattern. Each rhombus shares a side with the rhombus next to it. This creates a continuous ring of rhombuses that forms the six sides of the hexagon.
Imagine you’re holding a rhombus in your hand. Now, carefully place another rhombus next to it, sharing one of its sides. Continue adding rhombuses, always making sure that each new rhombus shares a side with the one before it. After adding six rhombuses, you’ll have a beautiful hexagon!
Steps to Build a Hexagon
Here are the steps you can follow to build a hexagon using rhombuses:
- Start with one rhombus. This will be the foundation of your hexagon.
- Place another rhombus next to the first rhombus, sharing one of its sides. You should now have two rhombuses connected side by side.
- Continue adding rhombuses one at a time, always making sure that each new rhombus shares a side with the previous one. You’ll notice that as you add rhombuses, they start to form a circular shape.
- After adding the sixth rhombus, you’ll have a complete hexagon. The six sides of the hexagon will be formed by the six sides of the rhombuses. You’ve successfully built a hexagon using rhombuses!
Exploring Different Hexagon Sizes

So far, we’ve built a hexagon using four rhombuses. But what happens when we want to create a bigger hexagon? Let’s dive into the exciting world of scaling up our hexagon creations!
Relationship Between Side Length and Number of Rhombuses
Let’s examine the connection between the size of a hexagon and the number of rhombuses required to build it. Imagine you’re a construction worker, and your rhombuses are the building blocks for a magnificent hexagon city. The longer the side of your hexagon city, the more building blocks you’ll need.
- Imagine a hexagon with a side length of 2 rhombuses. You’ll need 6 rhombuses to create each side, resulting in a total of 12 rhombuses for the entire hexagon.
- Now, let’s imagine a bigger hexagon with a side length of 3 rhombuses. You’ll need 9 rhombuses to create each side, leading to a grand total of 27 rhombuses to complete this majestic hexagon city.
You might notice a pattern emerging! The number of rhombuses required to build a hexagon increases as the side length increases. Let’s make this observation more concrete:
The number of rhombuses needed for a hexagon is equal to the side length of the hexagon squared, multiplied by 3.
This formula can be expressed mathematically as:
Number of Rhombuses = (Side Length)² – 3
Using this formula, we can predict the number of rhombuses needed for any hexagon size. For example, a hexagon with a side length of 4 rhombuses would require (4)² – 3 = 48 rhombuses.
Through this exploration, we’ve discovered that the number of rhombuses needed to create a hexagon depends on the size of the hexagon. By understanding the relationship between the side length of a hexagon and the number of rhombuses required, we can predict the number of rhombuses needed for any size hexagon. This knowledge not only helps us in building hexagons but also provides a foundation for understanding other geometric concepts and patterns.
FAQs: How Many Pattern Block Rhombuses Would Create 4 Hexagons
What is the difference between a rhombus and a hexagon?
A rhombus is a four-sided shape with all sides equal in length, while a hexagon is a six-sided shape with all sides equal in length. The angles of a rhombus are not all equal, whereas a hexagon has equal angles.
How many rhombuses are needed to create a hexagon with a side length of 1 rhombus?
Six rhombuses are needed to create a hexagon with a side length of 1 rhombus.
What is the relationship between the side length of a hexagon and the number of rhombuses needed?
The number of rhombuses needed to create a hexagon is equal to the square of the side length of the hexagon. For example, a hexagon with a side length of 2 rhombuses requires 4 rhombuses (2 squared) to construct.






