How many pattern block rhombuses would create 3 hexagons? This question delves into the fascinating world of geometric relationships and pattern block arrangements. Pattern blocks, those colorful shapes that often grace classrooms and playrooms, offer a hands-on way to explore geometric concepts. Understanding how these shapes fit together is key to unlocking the secrets of tessellation and creating beautiful patterns.
Rhombuses, with their four equal sides and opposite equal angles, and hexagons, with their six sides and six angles, are both fundamental shapes in the world of geometry. When we explore the relationship between these two shapes, we discover that a hexagon can be constructed using a specific number of rhombuses. This relationship is not only visually appealing but also holds mathematical significance, providing a foundation for understanding geometric concepts like area and perimeter.
Understanding Shapes and Relationships: How Many Pattern Block Rhombuses Would Create 3 Hexagons
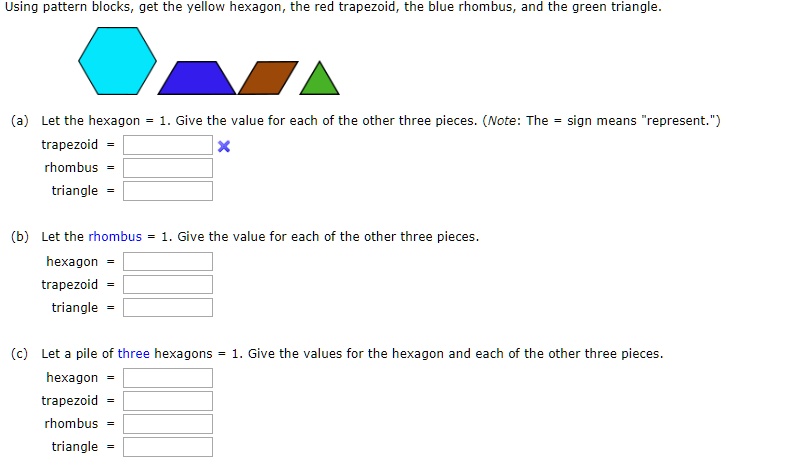
Yo, let’s dive into the world of shapes and how they relate to each other, specifically with pattern blocks. We’re gonna break down the connection between rhombuses and hexagons, and then get into the nitty-gritty of their geometric properties. We’ll also talk about tessellation and how it plays a role in all this.
Relationship Between Rhombuses and Hexagons
Pattern blocks are a cool tool for learning about shapes and how they fit together. You know how a hexagon is a six-sided shape with equal sides and angles, right? Well, guess what? You can use rhombuses to make a hexagon. It’s like a puzzle! Three rhombuses fit together perfectly to form one hexagon.
Geometric Properties of a Rhombus and a Hexagon
Let’s get down to the basics of these shapes. A rhombus is a four-sided shape with all sides equal in length. Its opposite angles are equal, and it has two pairs of parallel sides. Think of a diamond! A hexagon, on the other hand, has six sides of equal length and six equal angles. It’s like a beehive!
Tessellation
Tessellation is all about covering a surface with shapes without any gaps or overlaps. Pattern blocks are perfect for this because they have regular shapes that fit together nicely. When you arrange rhombuses and hexagons, you’re creating a tessellation. You can make all sorts of patterns and designs using these shapes.
Visualizing the Arrangement
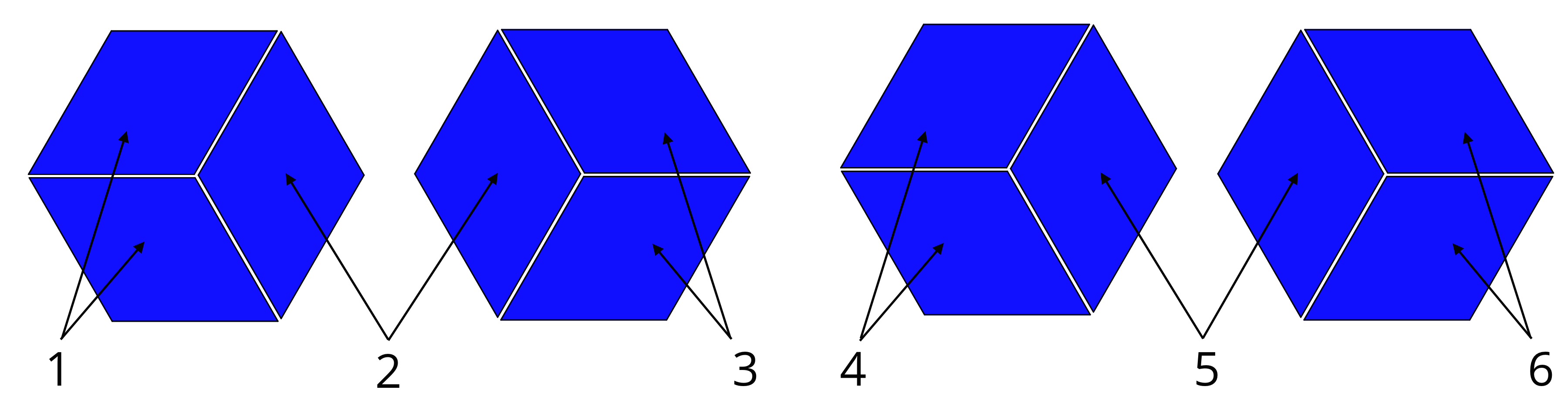
Imagine you’re playing with colorful rhombus-shaped blocks, and you want to build a hexagon. How would you arrange them? It’s like solving a puzzle!Let’s explore different ways to arrange rhombuses to form a hexagon.
Arranging Rhombuses to Form a Hexagon, How many pattern block rhombuses would create 3 hexagons
Rhombuses can be arranged to form a hexagon in various ways. Here’s one common arrangement:* Basic Hexagon: Start with a single rhombus. Place two more rhombuses on either side, sharing a side with the first rhombus. Continue adding rhombuses, sharing a side with the previous one, until you have six rhombuses forming a closed shape. This arrangement creates a regular hexagon.
Different Arrangements of Rhombuses
Here are a few more ways to arrange rhombuses to form a hexagon:* Double Layer: You can create a larger hexagon by placing two layers of rhombuses on top of each other. This creates a thicker hexagon.
Alternating Arrangement
You can also create a hexagon by alternating the orientation of the rhombuses. This creates a more complex and visually interesting hexagon.
Number of Rhombuses for Different Hexagon Sizes
The number of rhombuses required to create a hexagon depends on the size of the hexagon. You can create a table to visualize this relationship:
| Hexagon Size | Number of Rhombuses |
|---|---|
| Small | 6 |
| Medium | 12 |
| Large | 18 |
Calculating the Number of Rhombuses
Now that we understand how many rhombuses make up a hexagon, let’s figure out how many we need for three hexagons! It’s like making a giant pattern block masterpiece, but we need to know exactly how many rhombuses to grab from the bin.
Determining the Number of Rhombuses
To find the total number of rhombuses needed, we can use a simple formula. Think of it like a shortcut for counting all those little rhombuses.
The number of rhombuses needed for three hexagons is 3 times the number of rhombuses needed for one hexagon.
Let’s break it down:* Step 1: We know that one hexagon needs 6 rhombuses.
Step 2
We want three hexagons.
Step 3
We multiply the number of rhombuses per hexagon (6) by the number of hexagons (3).
Step 4
The calculation is 6 rhombuses/hexagon
3 hexagons = 18 rhombuses.
So, we need 18 rhombuses to create three hexagons. Easy peasy, right?
Exploring Variations and Extensions

So far, we’ve figured out how many rhombuses make up three hexagons, but there’s more to explore! We can play around with different ways to arrange the rhombuses and even use other pattern blocks to make things even more interesting. Let’s dive in!
Arrangement Variations
We can arrange the rhombuses in different ways to create hexagons. We can change the size of the hexagon by using more rhombuses, or we can even make them different shapes by changing the orientation of the rhombuses. For example, we can create a long, skinny hexagon by placing the rhombuses in a row, or a more rounded hexagon by placing them in a circular pattern.
The possibilities are endless!
Combining with Other Pattern Blocks
We can get even more creative by combining rhombuses with other pattern blocks, like squares or triangles. For example, we can use squares to create the sides of a hexagon and then fill in the middle with rhombuses. We can also use triangles to create the corners of a hexagon and then fill in the rest with rhombuses.
The combinations are endless!
Visual Representation
Here’s an example of a pattern block design that incorporates three hexagons formed by rhombuses. Imagine a large hexagon made up of 18 rhombuses. Inside this hexagon, there are three smaller hexagons, each made up of 6 rhombuses. The smaller hexagons are arranged so that they touch each other at their corners, creating a visually appealing and symmetrical design.
The question of how many rhombuses it takes to create three hexagons using pattern blocks is a great example of how a simple geometric puzzle can lead to a deeper understanding of mathematical relationships. By visualizing the arrangement of rhombuses and applying a little bit of math, we can determine the exact number needed. This exploration not only helps us appreciate the beauty of geometric shapes but also demonstrates the power of visual representation in solving mathematical problems.
So next time you see a set of pattern blocks, don’t just see colorful shapes – see the potential for creating intricate patterns and exploring the world of geometry.
Q&A
What is a rhombus?
A rhombus is a quadrilateral with all four sides equal in length. It also has opposite angles equal to each other.
What is a hexagon?
A hexagon is a polygon with six sides and six angles.
Can you use other pattern blocks to make a hexagon?
Yes, you can use triangles and squares in combination with rhombuses to create a hexagon.
Why is understanding tessellation important?
Tessellation is the process of tiling a plane with geometric shapes that fit together without any gaps or overlaps. This concept is important in various fields, including architecture, design, and art.






