Why does atomic radius decrease from left to right? That’s the million-dollar question in the periodic table’s drama! As we journey across a period, from alkali metals to noble gases, something sneaky happens to the size of these atoms. It’s a tale of nuclear pull, electron shielding, and sibling rivalry – a microscopic tug-of-war that dictates how these elements behave and interact.
Get ready to dive into the atomic-sized action!
Atomic radius, simply put, is the distance from the atom’s nucleus to its outermost electron. Across a period, the number of protons in the nucleus increases, boosting the positive charge. This stronger positive pull from the nucleus tugs the electrons closer, shrinking the atom. However, the story isn’t that simple. Electrons aren’t just passive players; they also repel each other.
This interplay between nuclear attraction and electron repulsion, along with the shielding effect of inner electrons, determines the final atomic size. We’ll unpack each of these forces to understand why atoms get smaller as we move across the periodic table.
Introduction to Atomic Radius
Atomic radius is a fundamental concept in chemistry that describes the size of an atom. While it’s not a precisely defined value due to the fuzzy nature of electron clouds, it’s crucial for understanding various chemical properties and behaviors, including reactivity, bonding, and the physical properties of substances. Understanding atomic radius helps us predict how atoms will interact with each other.
Periodic trends, the regular patterns of properties across the periodic table, are largely driven by changes in atomic size.Atomic size isn’t static; it varies systematically across the periodic table. This variation is influenced by several factors working in concert, leading to predictable patterns. We can generally observe that atomic radius increases as we move down a group and decreases as we move across a period (from left to right).
However, the interplay of these influencing factors sometimes leads to exceptions to this general trend.
Factors Influencing Atomic Size
Several key factors determine an atom’s size. The primary factors are the number of electron shells (energy levels) and the effective nuclear charge experienced by the outermost electrons. As we move down a group, we add more electron shells, leading to a larger atomic radius. Conversely, as we move across a period, the number of protons in the nucleus increases, increasing the positive charge pulling the electrons closer, thus decreasing the atomic radius.
However, the addition of electrons to the same shell partially shields the outer electrons from this increased nuclear charge. This shielding effect, while not completely neutralizing the increased nuclear charge, partially mitigates the decrease in atomic radius.The effective nuclear charge, experienced by the valence electrons, is a critical factor. It represents the net positive charge felt by these outermost electrons after accounting for the shielding effect of inner electrons.
A higher effective nuclear charge leads to a stronger pull on the valence electrons, resulting in a smaller atomic radius. Conversely, a lower effective nuclear charge allows the valence electrons to be further from the nucleus, resulting in a larger atomic radius. The balance between the addition of electron shells and the increase in effective nuclear charge dictates the overall trend in atomic radius across the periodic table.
For instance, consider the difference between Lithium (Li) and Fluorine (F). Both are in the same period, but F has a much higher effective nuclear charge, resulting in a significantly smaller atomic radius than Li.
Effective Nuclear Charge and Atomic Radius

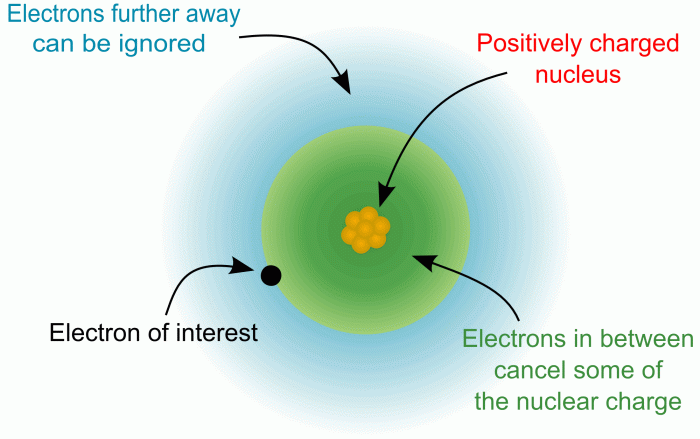
Atomic radius trends across the periodic table are largely explained by the interplay between the number of protons in the nucleus and the shielding effect of inner electrons. Understanding effective nuclear charge is key to grasping why atomic radius decreases across a period.Effective nuclear charge (Z eff) represents the net positive charge experienced by an electron in a multi-electron atom.
It’s not simply the total positive charge of the nucleus (the atomic number, Z), because inner electrons shield outer electrons from the full pull of the protons. Think of it like this: the inner electrons act like a buffer, partially blocking the outer electrons’ view of the positively charged nucleus.
Effective Nuclear Charge and Electron Attraction
The stronger the effective nuclear charge, the greater the attraction between the nucleus and the valence electrons. This stronger pull draws the valence electrons closer to the nucleus, resulting in a smaller atomic radius. Conversely, a weaker effective nuclear charge leads to a weaker attraction, allowing the valence electrons to exist further from the nucleus and resulting in a larger atomic radius.
The difference in Zeff across a period directly influences the size of atoms.
Effective Nuclear Charge Across a Period
Across a period, the number of protons increases, while the principal quantum number (n) of the valence electrons remains constant. This means that while more protons are added, increasing the positive charge, the shielding effect provided by the added electrons in the same energy level is relatively small. The increase in nuclear charge significantly outweighs the increase in shielding, leading to a substantial increase in Zeff.
This stronger effective nuclear charge pulls the valence electrons closer to the nucleus, resulting in a decrease in atomic radius.
Period 3 Effective Nuclear Charge Comparison
The following table illustrates the trend of increasing effective nuclear charge across Period 3. Note that precise values of Zeff require advanced calculations, and these are approximate values to illustrate the trend.
| Element | Atomic Number (Z) | Number of Protons | Approximate Effective Nuclear Charge (Zeff) |
|---|---|---|---|
| Na | 11 | 11 | 2.5 |
| Mg | 12 | 12 | 3.5 |
| Al | 13 | 13 | 4.5 |
| Si | 14 | 14 | 5.5 |
| P | 15 | 15 | 6.5 |
| S | 16 | 16 | 7.5 |
| Cl | 17 | 17 | 8.5 |
| Ar | 18 | 18 | 9.5 |
Shielding Effect and Atomic Radius
The shielding effect, also known as the screening effect, plays a crucial role in determining an atom’s size. It describes how inner electrons reduce the attractive force of the nucleus on outer electrons. This reduction in the felt nuclear charge directly impacts the atomic radius.Inner electrons, those closer to the nucleus, effectively block the positive charge of the protons from reaching the outer electrons.
Think of it like this: the inner electrons form a cloud of negative charge that partially neutralizes the positive charge of the nucleus. The outer electrons experience a weaker pull from the nucleus than they would if the inner electrons weren’t there. This weaker attraction allows the outer electrons to exist at a greater average distance from the nucleus, leading to a larger atomic radius.
Shielding Effect Across a Period
Across a period (moving left to right on the periodic table), the number of protons increases, while the number of inner electron shells remains constant. This means that the effective nuclear charge increases significantly as you move across a period, even though the shielding effect provided by the inner electrons remains relatively the same. The increase in positive charge pulls the outer electrons closer, leading to a decrease in atomic radius.
For example, lithium (Li) has a larger atomic radius than fluorine (F) because, despite the similar shielding from the 1s electrons, the significantly greater nuclear charge of fluorine pulls its valence electrons much closer.
Shielding Effect and Effective Nuclear Charge
The shielding effect is intrinsically linked to the effective nuclear charge (Z eff). Z eff represents the net positive charge experienced by an electron after accounting for the shielding effect of other electrons. It’s calculated as the difference between the actual nuclear charge (number of protons) and the shielding constant (representing the shielding effect). A higher Z eff indicates a stronger attraction between the nucleus and the outer electrons, resulting in a smaller atomic radius.
Conversely, a lower Z eff, due to a stronger shielding effect, results in a larger atomic radius. The relationship can be represented conceptually as:
Zeff = Z – S
where Z is the nuclear charge and S is the shielding constant. The greater the shielding (larger S), the smaller the effective nuclear charge (Z eff) and consequently, the larger the atomic radius.
Electron-Electron Repulsion and Atomic Radius: Why Does Atomic Radius Decrease From Left To Right
Okay, so we’ve talked about how the nucleus pulls on electrons, but electrons also repel each other. This repulsion plays a surprisingly big role in how big an atom actually is. Think of it like a tug-of-war: the nucleus is pulling inward, and the electrons are pushing outward. The balance between these forces determines the atomic radius.Electron-electron repulsion is the force that exists between electrons in the same atom.
Because electrons have the same negative charge, they naturally repel each other. This repulsion counteracts the attractive force of the positively charged nucleus, making the atom slightly larger than it would be if only nuclear attraction were considered. The more electrons an atom has, the greater the overall electron-electron repulsion. This effect is particularly significant when considering atoms across a period.
Electron-Electron Repulsion Across a Period, Why does atomic radius decrease from left to right
Across a period, the number of protons in the nucleus increases, leading to a stronger nuclear charge. However, the added electrons are all going into the same principal energy level (same shell). This means that the extra electrons are added to the same general region of space, leading to increased electron-electron repulsion. While the increased nuclear charge pulls the electrons closer, the increased repulsion pushes them further apart.
The net effect across a period is that the increase in nuclear charge dominates over the increase in electron-electron repulsion, resulting in a decrease in atomic radius.
Visual Representation of Electron-Electron Repulsion
Imagine a series of diagrams representing the electron clouds of atoms across a period, say, from lithium (Li) to neon (Ne). Each diagram would show a nucleus at the center, surrounded by electron clouds representing the different energy levels. The size of the nucleus would increase gradually across the period to reflect the increasing number of protons. The electron clouds themselves would also become slightly more dense to represent the increase in the number of electrons.
However, the crucial element is illustrating the increased crowding of electrons in the outermost shell as we move across the period. We can visually depict this crowding by showing the outermost electron cloud becoming more compressed, despite the increasing nuclear charge. The compression reflects the increased electron-electron repulsion in this outermost shell. For instance, lithium’s outermost electron cloud would appear relatively diffuse, while neon’s would appear more compact and tightly packed, even though the neon nucleus is significantly smaller than the lithium nucleus.
The difference in the compactness of the outermost electron cloud would be the visual representation of the increasing electron-electron repulsion, despite the decrease in atomic radius.
Atomic Radius Across a Period
Okay, so we’ve talked about atomic radius in general, and now let’s dive intowhy* it shrinks as we move from left to right across a period on the periodic table. It’s all about the interplay of several factors, and understanding their relative strengths is key.
The decrease in atomic radius across a period is a fundamental trend in chemistry, directly linked to the increase in effective nuclear charge and the relatively minor changes in shielding and electron-electron repulsion.
Effective Nuclear Charge and Atomic Radius
The dominant force driving the decrease in atomic radius across a period is the increase in effective nuclear charge (Z eff). Remember, Z eff is the net positive charge experienced by the outermost electrons. As we move across a period, the number of protons in the nucleus increases, while the number of shielding inner electrons remains relatively constant (they’re all in the same principal energy level).
This means the outermost electrons are pulled more strongly towards the increasingly positive nucleus.
- For example, consider the elements Lithium (Li) and Beryllium (Be). Both have electrons in the same energy level, but Be has one more proton. This extra proton increases the effective nuclear charge experienced by the valence electrons in Be, pulling them closer to the nucleus and resulting in a smaller atomic radius for Be compared to Li.
- This trend continues across the period. Each subsequent element adds a proton, increasing Z eff and further shrinking the atomic radius.
Shielding Effect and Atomic Radius
While the shielding effect (the reduction of the nuclear charge by inner electrons) does play a role, its influence is relatively minor across a period. The electrons added across a period are all in the same energy level, and therefore provide minimal shielding to each other. The increased nuclear charge outweighs the small increase in shielding.
Electron-Electron Repulsion and Atomic Radius
Electron-electron repulsion, the force of electrons repelling each other, also plays a role, but it’s less significant than the increase in effective nuclear charge. While the addition of electrons increases repulsion, this effect is outweighed by the stronger pull of the increasing nuclear charge. The electrons are added to the same energy level, so the increase in repulsion is not as dramatic as the increase in the attractive force from the nucleus.
Examples of Atomic Radius Trends
Let’s look at some concrete examples to solidify our understanding of how atomic radius changes across a period. We’ll focus on elements in the second period of the periodic table, where the trend is particularly clear. Remember, atomic radius generally decreases as we move from left to right across a period.The increase in effective nuclear charge, with the addition of protons without a corresponding increase in shielding, pulls the electrons closer to the nucleus, resulting in a smaller atomic radius.
This trend isn’t always perfectly smooth, however, and some slight deviations can occur.
Atomic Radii in the Second Period
We can compare the atomic radii of the elements lithium (Li), beryllium (Be), boron (B), carbon (C), nitrogen (N), oxygen (O), fluorine (F), and neon (Ne). Moving from left to right, we observe a consistent decrease in atomic radius. Lithium, with its single valence electron, has the largest atomic radius in this period. As we add protons and electrons, the effective nuclear charge increases, pulling the electrons closer to the nucleus.
Neon, with its full valence shell, has the smallest atomic radius. Approximate atomic radii are: Li (152 pm), Be (112 pm), B (87 pm), C (77 pm), N (75 pm), O (73 pm), F (71 pm), Ne (69 pm). Note that these values can vary slightly depending on the measurement method and source.
Exceptions to the General Trend
While the general trend of decreasing atomic radius across a period is very reliable, there can be small, subtle irregularities. These often stem from electron-electron repulsions within the same subshell. For instance, while the trend holds true for the second period, some minor fluctuations can be seen. The slight increase in atomic radius between nitrogen (N) and oxygen (O) is a common example.
This is because of the electron configuration. Oxygen’s addition of a second electron to the 2p subshell leads to increased electron-electron repulsion, slightly counteracting the effect of the increased nuclear charge. This repulsion pushes the electrons slightly further apart, leading to a marginally larger atomic radius for oxygen compared to what might be strictly predicted based on the increasing nuclear charge alone.
The difference is small, but it demonstrates the complexity of atomic interactions. Similar, though smaller, effects can be observed in other periods. It is crucial to remember that these are relatively minor deviations from the overall trend.
Array
Knowing how atomic radius changes across the periodic table isn’t just an academic exercise; it’s a powerful tool for predicting and understanding a huge range of chemical and material properties. The size of an atom directly influences how it interacts with other atoms, determining its reactivity and the types of bonds it forms. This knowledge is crucial in fields ranging from materials science to drug design.Understanding atomic radius trends allows us to predict chemical properties because atomic size directly impacts several key factors influencing chemical behavior.
Smaller atoms tend to have higher ionization energies, meaning they hold onto their electrons more tightly, making them less likely to form positive ions. Conversely, larger atoms often have lower ionization energies and greater electron affinities, leading to a higher propensity to form negative ions or share electrons readily. This interplay between size and electron behavior directly dictates reactivity and bond formation.
Atomic Size’s Influence on Reactivity and Bonding
Atomic radius plays a significant role in determining the reactivity and types of bonds an element forms. For instance, the highly reactive alkali metals (like sodium and potassium) have large atomic radii, making it relatively easy to remove their outermost electron, resulting in the formation of +1 ions. In contrast, halogens (like chlorine and fluorine), with smaller atomic radii and high electron affinities, readily gain an electron to achieve a stable electron configuration, forming -1 ions.
The size difference also impacts the strength and nature of the bonds formed. Smaller atoms generally form stronger covalent bonds due to increased orbital overlap, while larger atoms might favor weaker interactions. Consider the difference between the strong bonds in water (H₂O), where the small oxygen atom facilitates strong interactions, and the weaker interactions in hydrogen sulfide (H₂S), where the larger sulfur atom leads to weaker bonds.
Atomic Radius in Material Science
The applications of atomic radius understanding extend significantly into materials science. For example, the properties of semiconductors, crucial components in electronics, are heavily dependent on the atomic radii of the constituent elements. Variations in atomic size within a semiconductor material can alter its band gap, influencing its electrical conductivity and making it suitable for specific applications. Similarly, the strength and durability of alloys are influenced by the atomic radii of the metals involved.
If the atomic radii of the alloying elements are significantly different, it can lead to lattice distortions, affecting the material’s overall strength and other mechanical properties. The development of new materials with specific properties often requires careful consideration of the atomic radii of the constituent elements to fine-tune the desired characteristics. For instance, the design of high-strength steel involves carefully selecting alloying elements with atomic radii compatible with iron to create a strong and durable material.
So, there you have it – the atomic-sized mystery solved! The decrease in atomic radius across a period is a consequence of the increasing effective nuclear charge dominating the effects of electron shielding and repulsion. This seemingly small change in size has huge consequences for the chemical properties and reactivity of elements. Understanding this fundamental trend unlocks a deeper appreciation for the periodic table and the amazing world of chemistry! Now go forth and amaze your friends with your newfound atomic knowledge!
Helpful Answers
What are some real-world applications of understanding atomic radius trends?
Understanding atomic radius is key to predicting how elements will bond and react. It helps us design new materials with specific properties, like superconductors or stronger alloys.
Are there any exceptions to the general trend of decreasing atomic radius across a period?
Yes, there are some minor exceptions, usually due to electron configurations and subtle variations in electron-electron repulsion. These exceptions are usually explained by the specific electron arrangements.
How does atomic radius relate to ionization energy?
Smaller atoms generally have higher ionization energies because the outer electrons are more strongly attracted to the nucleus, making them harder to remove.
Why is the effective nuclear charge important in determining atomic radius?
The effective nuclear charge represents the net positive charge experienced by valence electrons. A higher effective nuclear charge means a stronger pull from the nucleus, resulting in a smaller atomic radius.





